

Länk till: Del 1, Del 2, Del 3, Del 5
Hur fungerar jordplan egentligen?
Del 4. (Publicerat i emc MAGAZINE nr 3, 1999)Torbjörn Karlsson, Emicon.
I tidigare avsnitt har vi försökt beskriva de mekanismer som gör att jordplan kan användas för att minska störningar. Nu ska vi se hur en signal på en ledning kan förhindras att koppla över till en näraliggande ledning. Det fenomen som vi vill bekämpa brukar av historiska, akustiska, skäl kallas överhörning eller på engelska crosstalk.
Vi ska visa hur jordplanets egenskaper utnyttjas för att förbättra signalöverföringen och minska överhörningen mellan ledare 1 och ledare 2 i figur 1. Ledarna, som har längden 1 dm, har bredden 2 mm och befinner sig 0,4 mm ovanför ett jordplan. Vi avslutar ledarna med motstånd i båda ändar så att RL1 = RL2 = RK1 = RK2 =100 W och RL12 = RK12 = ¥ (öppet). I källändan (K) matas en spänningspuls med amplitud 1 V in i ledare 1. Pulsen är nästan fyrkantig och varar i 10 ns. Pulsens stigtid och falltid är 0,5 ns.


Figur 1. Ledningens tvärsnitt med två plattledare med bredden 2 mm över ett jordplan med bredden 1 cm. Till höger visas en ledning med längden 1 cm, för att visa motstånden i ändarna. Beräkningen är utförd på en ledning med längden 10 cm.
I laständan (L) kan vi registrera spänningarna som visas i figur 2. Pulsen på ledare 1 har minskat till hälften på grund av spänningsdelning mellan källimpedans och lastimpedans. Dessutom har stigtiden påverkats på grund av reflektioner på ledningen. På ledare 2 kan vi se en störning som har amplituden 5 mV.

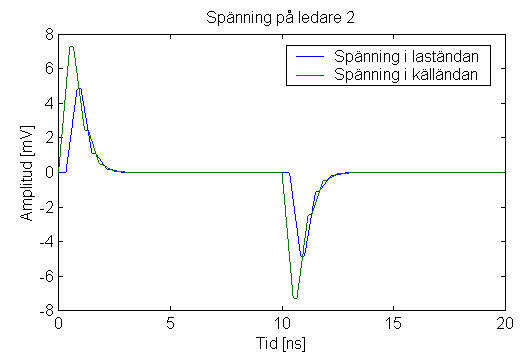
Figur2. Spänning i laständan på ledningen enligt figur 1 då en spänningspuls med amplituden 1 V matas in på ledare 1 i källändan.
Vi minskar nu ledarnas höjd över jodplanet så att den blir hälften så stor som tidigare, figur 3. Den överkopplade pulsen på ledare 2 blir då ungefär hälften så stor, figur 4.

Figur 3. Ledarnas höjd över jordplanet har minskats till hälften jämfört med ledningen i figur 1.
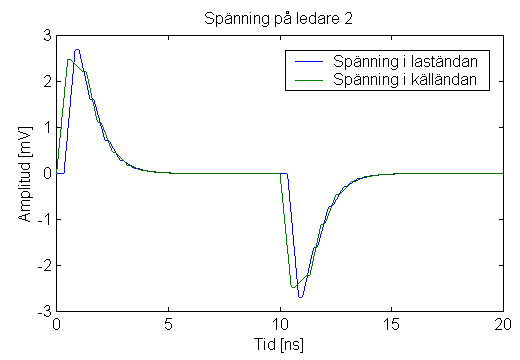
Figur 4. Den överkopplade spänningen har minskat till ungefär hälften av vad den är i figur 2.
Minskningen kan delvis förklaras med att kapacitansen mellan ledarna och den ömsesidiga induktansen mellan ledarna har ökat, som vi har sett i tidigare avsnitt. Men det finns ytterligare en viktig faktor som förutsätter att jordplanet finns, och det är att ledarna nu bildar en transmissionsledning med konstanta förhållanden utefter ledningen. Vi säger att ledningen har en karakteristisk impedans vilket är en sorts impedansreferens att jämföra kopplingsimpedanser och avslutningsimpedanser med. För en 2 -ledare över jordplan beskrivs karakteristiska impedansen av en 2 x 2 matris Zij där Z12 = Z21 . Värdena i matrisen går att översätta till delimpedanser så att ledningen i figur 3 har de karakteristiska delimpedanserna 29,8 W mellan varje ledare och jord samt 2 kW mellan ledarna. Om vi börjar med att ändra RL1 i ledare 1 till 29,8 W kommer detta att påverka signalöverföringen på ett gynnsamt sätt, pulsen kommer fram nästan oförstörd, figur 5. Nivån har gått ned på grund av spänningsdelning mellan RK1 och RL1 . Genom att sätta RL2 = 29,8 W på ledare 2 kommer den överkopplade störningen att minska något i laständan och få ett annat utseende, figur 6.
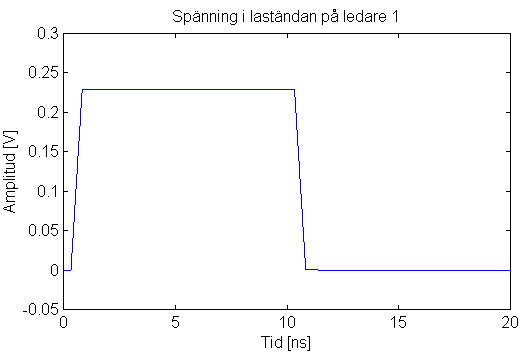
Figur 5. Spänningspuls i laständan på ledare 1 med RL1 = 29,8
W
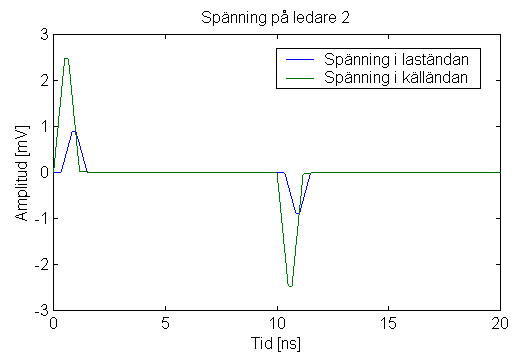
Figur 6. Överkopplad spänningspuls på ledare 2 med RL2 = 29,8
W
Den radikala lösningen är att sätta även RK1 = RK2 = 29,8
W och RK12 = RL12 = 2 kW . Då kommer överhörningen att försvinna helt, figur 7.Vi har nu åstadkommit en perfekt avslutning av transmissionsledningen i båda ändar. En förutsättning för att man ska kunna göra detta är förstås att man har ett jordplan, som skapar en transmissionsledning och som erbjuder en referens att ansluta avslutningsmotstånden till.
Denna ideala, helt störningsfria, lösning kräver bland annat att ledningen har en omgivning där det inte finns material med olika dielektricitetskonstant. Vi återkommer till det.
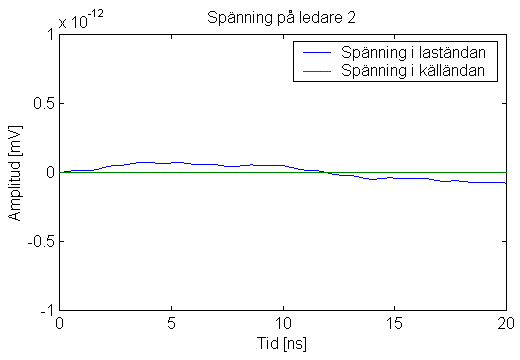
Figur 7. Den överkopplade störningen försvinner helt när ledningen avslutas i båda ändar med impedanser som motsvarar ledningens karakteristiska impedans. Den blå kurvan visar den numeriska onoggrannheten på ca 10-16 V.
Läsarna är välkomna till www.emicon.com. för att kostnadsfritt hämta det program som använts för att räkna fram ovanstående kurvor. Programmet bygger på formler som kan återfinnas i boken:
Tesche, Ianoz, Karlsson: "EMC Analysis Methods and Computational Models", kapitel 6.